top of page
Summary: 
Regarding some already exposed concepts of the modelling routine:
From page          we got our model 
03_Hzke.png
01_abx.png
or 
Where the Heads ( h ) equal (k), plus a error; all being mediated the Z matrix
It's inverse notation                          gives
the (k) parameters we need to reach 
04+kz-1.png
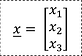
05.png
Let's us advance in some more concepts: 
From the 3-dimentinal vector: 
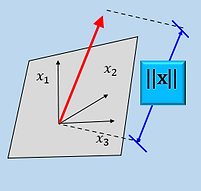
24_equation.PNG
Comes its norm or magnitude
||X|| , as well, 
concepts of 
unity (1) and
​orthogonality
Meanwhile, the "covariance" model (Z) between the effective observations (h) and parameters (k) can also be described by the SVD notation: 
22_equation.PNG

Beta μ

It can be done because any square matrix can be seen also in terms of its canonical form, the matrixes: modal; “diagonal”; and transpose modal. 

Recall the concepts of eigenvalues and eigenvectors presented in page 09.

Nevertheless, MS Excel add-ins reach the same results in: 
26_equation.PNG
So much so, we here expeditiously introduce the implications the Partitioning of Orthonormal Matrix
Where every column is orthogonal to every other column and every column is a unit vector.
25_equation.PNG
23_equation.PNG
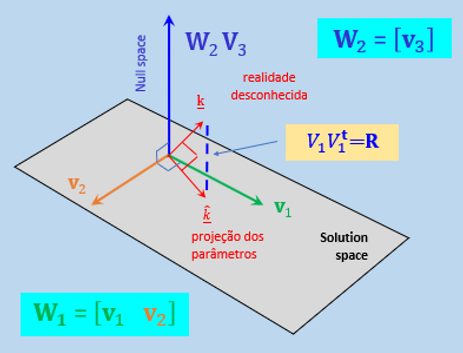
27_equation.PNG

A [transpose V matrix partition] for instance, entails a 2D [solution subspace] spanned by the V1 and V2 vectors. 
A little more complicated, there is also a 1D [Null subspace] spanned by V3 (or W2) vector.  

Solution and Null spaces, correlated vectors and projections of these vectors, will be discussed henceforth.
bottom of page